DUSSON Alexandre
|
BENOIT Christophe DUSSON Alexandre |
MPSI |
TIPE sur la compression de données informatiques
I- Problèmes concrets et utilisation de la compression de données
La compression de données informatiques consiste à réduire la taille de l'information pour le stockage de cette information et son transport.
Exemples d’utilisation de la compression pour le stockage :
Le coût et les limites technologiques nécessitent d’utiliser la compression de données pour le stockage d’importants volumes d’information.
Exemples d’utilisation de la compression pour le transport :
Pour une durée donnée, la compression permet de faire circuler plus d’informations, le débit est donc plus grand.
On distingue pour cela deux types de compression suivant leur usage :
Les différents algorithmes de compression sont choisis en fonction de :
II- Compression sans perte
1. RLE (Run Length Encoding)
- Recherche des caractères répétés plus de n fois (n fixé par l'utilisateur)
- Remplacement de l'itération de caractères par:
Durant la lecture du fichier compressé, lorsque le caractère spécial est reconnu, on effectue l’opération inverse de la compression tout en supprimant ce caractère spécial.
ex: AAAAARRRRRROLLLLBBBBBUUTTTTTT
On choisit comme caractère spécial : @ et comme seuil de répétition : 3
Après compression : @5A@6RO@4L@5BUU@6T gain : 11 caractères soit 38%
Cet algorithme utilise une bibliothèque c’est-à-dire une table de données contenant des chaînes de caractères.
Au cours du traitement de l’information, les chaînes de caractères sont placées une par une dans la bibliothèque. Lorsqu’une chaîne est déjà présente dans la bibliothèque, son code de fréquence d’utilisation est incrémenté.
Les chaînes de caractères ayant des codes de fréquence élevés sont remplacées par un " mot " ayant un nombre de caractères le plus petit possible et le code de correspondance est inscrit dans la bibliothèque.
On obtient ainsi une information encodée et sa bibliothèque.
Lors de la lecture de l’information encodée, les " mots " codés sont remplacés dans le fichier par leur correspondance lue dans la bibliothèque et le fichier d’origine est ainsi reconstitué.
Cette méthode est peu efficace pour les images mais donne de bons résultats pour les textes et les données informatiques en général (plus de 50%).
Construction de l’arbre : on relie deux à deux les caractères de fréquence les plus basses et on affecte à ce nœud la somme des fréquences des caractères. Puis on répète ceci jusqu'à ce que l’arbre relie toutes les lettres. L’arbre étant construit, on met un 1 sur la branche à droite du nœud et un 0 sur celle de gauche.
Exemple d’encodage de Huffman :
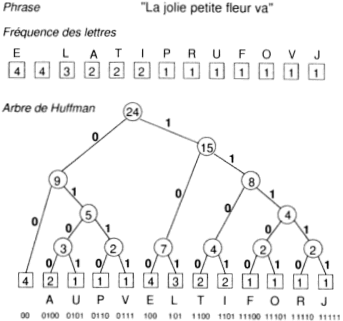
Le fichier compressé se compose d’une suite de codes sans séparateur, bien que les codes comportent un nombre variable de bits, car chaque code a la propriété d’unicité de son préfixe.
On transmet la bibliothèque de codage, puis on associe les caractères à leur code.
Cet algorithme permet de compresser aussi bien des images que des textes, on parle de compression statistique ou codage entropique (probabilités d’apparition d’un caractère). On obtient une compression satisfaisante (50% en moyenne) et un temps de compression assez rapide. En revanche il faut transmettre la bibliothèque en même temps, et il arrive que la taille du fichier soit plus grande que celle du fichier non compressé. De plus il est très sensible à la perte d’un bit, toutes les valeurs qui suivront ce bit seront fausses lors de la décompression.
III- Compression avec pertes
Pour les images :
Une dégradation de l’image décompressée – indiscernable à l’œil ou suffisamment faible pour être acceptable – est acceptée en contrepartie d’un taux de compression très élevé.
La norme J.P.E.G. définie en 1991 par un groupe d’experts du monde de la photographie est actuellement la méthode de compression d’images fixes avec pertes la plus utilisée.
Schéma de principe :

L’image d’origine est décomposée en blocs de 8´8 pixels (on obtient pour chaque bloc 64 coordonnées d’une matrice 8´8 correspondant chacune à une couleur). On applique à chaque matrice la transformation DCT (Transformée en Cosinus Discrète). Cette technique réversible est similaire à la transformée de Fourier qui transforme une image en une somme de fonctions sinus et cosinus de différentes fréquences et amplitudes, mais la DCT se contente des cosinus. Chaque carré est représenté par une somme de 64 fonctions cosinus de fréquences et d’amplitude appropriées à chacune desquelles on associe une matrice, on obtient ainsi une matrice tridimensionnelle 8´8´64. On observe que l’amplitude des composantes des basses fréquences (BF, c’est-à-dire ce qui correspond à une plage de couleur uniforme) est plus élevée que celle des composantes des hautes fréquences (HF, c’est-à-dire ce qui correspond à des variations brusques de couleur d’un pixel à l’autre). Les matrices sont ordonnées par leur fréquence (ou amplitude) et, pour schématiser, la compression consiste à retirer des détails pour diminuer le volume du fichier image en supprimant les hautes fréquences (HF), ce qui correspond à un filtre passe-bas. Le taux de compression va dépendre du seuil de l’écrêtage : plus on conserve des composantes à amplitude faible, meilleure sera la qualité (car plus il y aura de détails fins), mais plus faible sera le taux de compression.
Matrice tridimensionnelle :
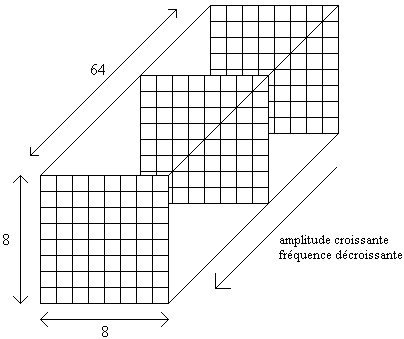
Pour simplifier l’étude, nous étudierons la somme de ces 64 matrices sous la forme d’une matrice à deux dimensions de type 8´8. Prenons pour exemple le bloc de 64 pixels extrait d’une image représenté dans la matrice 1, dont chaque coordonnée correspond à une couleur :
|
|
|
On applique ensuite la transformation DCT à la matrice 1 et on obtient la matrice 2.
Cette opération est totalement réversible et aucune information n’a été perdue à cette étape.
L’intérêt d’un telle transformation est que les coefficients de forte valeur absolue sont situés en haut et à gauche, l’importance des coefficients pour la reconstitution de l’image diminue quand on se déplace en diagonale vers le bas à droite.
L’étape suivante est la quantification qui donne des valeurs approximatives de la matrice 2 en tenant compte d’un pas de quantification prédéfini. Pour un pas de quantification Q, la valeur quantifiée est le quotient de la division euclidienne de la valeur par Q. (ex : pour un pas de quantification de 3, on remplace 0, 1et 2 par 0 ; 3, 4 et 5 par 1 …). C’est à cette étape que des pertes d’information apparaissent et la précision de l’image restituée est déterminée par le pas de quantification. Le pas de quantification est pris relativement petit pour les valeurs importantes (en haut à gauche) et il est de plus en plus grand au fur et à mesure que l’on descend vers le bas et la droite. L’ensemble des pas utilisés constituent ce que l’on appelle une matrice de quantification. Une matrice de quantification est construite en fonction de critères psycho-visuels, suivant la formule suivante : Q(i,j) = 1 + (1 + i + j) ´ Fq avec Fq facteur de qualité et Q le pas de quantification. Par exemple, pour Fq = 5 on obtient la matrice 3 (le facteur de qualité sera à indiquer au décodeur). Finalement, on prend la partie entière de la division de chaque valeur de la matrice 2 par la valeur de la matrice 3 ayant la même position et on obtient la matrice 4.
|
|
|
La matrice finale (matrice 4), possède beaucoup de 0 donc cette récurrence de valeurs sera compressée par un codage statistique tel que le codage de Huffman.
Le fichier est décompressé par la méthode de décodage statistique, puis la matrice obtenue est multipliée par la matrice de quantification que l’on reconstitue grâce au facteur de qualité et enfin on applique la DCT inverse pour retrouver une image plus ou moins dégradée par rapport à l’image initiale.
Cet algorithme fonctionne très bien avec des images à tons continus, son utilisation est moins agréable pour des images ayant de forts contrastes. Le taux de compression est très élevé : 90% avec une très bonne qualité et une vitesse de compression/décompression raisonnable. Lorsque le taux de compression est trop élevé, on a un effet mosaïque car l’image est divisée en petits carrés qui sont traités séparément ce qui fait apparaître les bords des différents carrés restitués.
Une image est formée de carrés de 256 pixels par 256 et chaque pixel est constitué de couleurs différentes. On peut donc modéliser cette image en une matrice carrée de 256 lignes et 256 colonnes où chaque coefficient représente le code d'une couleur.
On multiplie maintenant cette matrice par une matrice creuse (contenant beaucoup de zéros), du type :
|
A= |
|
Ex :
|
Soit M= |
|
Þ P=M´A= |
|
Dans la première moitié de la matrice on a l’échantillon principal, et dans la deuxième on a les détails. On veut maintenant effectuer cette opération sur les colonnes, pour ce fait on calcule N = tA ´ M ´ A. On applique maintenant le coefficient de précision à la matrice, c’est à dire que l’on supprime tous les coefficients inférieurs à e . On obtient maintenant une nouvelle matrice N ’ et pour retrouver la matrice originale on calcule M’ = tA-1 ´ N’ ´ A-1.
Mais ces calculs sont longs et on peut les réduire considérablement en remarquant que ![]() ´A est une matrice rectangulaire ( tA = A-1).
´A est une matrice rectangulaire ( tA = A-1).
Pour augmenter le taux de compression, on utilise plusieurs fois l’algorithme, mais on remarque que c’est toujours le quart de la matrice en haut à gauche qui comporte des coefficients nécessitant d’être réduits. L’algorithme est donc appliqué à cette partie.
Exemple : Nous allons compresser et décompresser la matrice suivante :
|
M = |
|
Soient A1, A2, A3 les matrices creuses :
| A1 = |
|
|
A2= |
|
A3= |
|
|
A = A1´ A2´ A3 = |
|
|
on calcule N = tA ´ M ´ A = |
|
|
on supprime tous les coefficients inférieurs à e : |
|
|
Pour décompresser, on calcule M’ = tA-1´ N’´ A-1 = |
|
On constate une faible différence entre la matrice originale et la matrice finale.
La compression par ondelette est une technique récente qui donne de très bons résultats, même avec des taux de compression élevés (plus de 90%). Cette méthode reste encore marginale par rapport à l'utilisation de JPEG, malgré ses avantages.
Les images fractales sont générées à partir d’une équation et de quelques paramètres. Si l’on veut compresser une telle image, il suffit de transmettre la formule qui l’a générée. Etant donnée une image quelconque, il est démontré à l’aide du théorème du point fixe l’existence et l’unicité d’une formule qui permette de reconstruire cette image, or il s’avère que la démonstration nous apporte une majoration permettant de trouver cette formule, nous avons ainsi une approximation de cette formule.
L’image est découpée en blocs de 16 pixels de côté qui sont à leur tour découpés en 4 blocs de 8 pixels de côté. Pour chaque bloc B, on détermine de manière approximative un couple de fonctions qui, lorsqu’on les applique une succession de fois, permettent à un bloc quelconque de converger vers ce bloc B, on parle alors d’attracteur.
On obtient un très fort taux de compression, encore plus important que celui de JPEG, mais son principal défaut est sa lenteur dans la phase de compression. Cette méthode fait encore l’objet de nombreuses recherches et, dans les années à venir, cette méthode remplacera le standard actuel JPEG.
Pour les vidéos :
Les vidéos sont constituées d’une succession d’images et, pour obtenir une animation, la différence entre deux images successives est minime. Le codage MPEG consiste à ne conserver que l’image de départ d’une animation, puis les modifications apportées à cette image. Lors d’un changement de plan, la première image de ce plan est conservée puis ses modifications. Les images sont également toutes compressées par la méthode JPEG.
Il existe également d’autres méthodes de compression pour les vidéos, ainsi que pour la compression de sons (codage MP3, PASC, …) mais leur étude n’a pas été traitée.
IV- Conclusion
La compression de données est appelée à prendre un rôle encore plus important en raison du développement des réseaux et du multimédia. Son importance est surtout due au décalage qui existe entre les possibilités matérielles des dispositifs que nous utilisons (débits sur Internet et sur les divers câbles, capacités des mémoires de masse, …) et les besoins qu’expriment les utilisateurs (visiophonie, vidéo plein écran, transfert de quantités d’information toujours plus importantes dans des délais toujours plus brefs). Quand ce décalage n’existe pas, ce qui est rare, la compression permet de toutes façons de faire des économies.
Les méthodes déjà utilisées couramment sont efficaces et sophistiquées (Huffman, LZW, JPEG) et utilisent des théories assez complexes. Les méthodes émergentes sont prometteuses (fractales, ondelettes) mais nous sommes loin d’avoir épuisé toutes les pistes de recherche. Les méthodes du futur sauront sans doute s’adapter à la nature des données à compresser et utiliseront l’intelligence artificielle.